BAB 5-Statistik (Statistics) II
Membina Carta Pai
Carta pai (pie chart) ialah perwakilan data dengan menggunakan luas sektor-sektor dalam sebuah bulatan.
Dalam sebuah carta pai, satu bulatan dibahagikan kepada sektor-sektor berlainan mengikut kuantiti setiap data.
Contohnya, rajah di bawah ialah satu carta pai yang meunjukkan murid-murid dalam setiap tingkatan di sebuah sekolah.
Bagi membina sebuah carta pai, satu bulatan dibahagikan kepada sektor-sektor berlainan mengikut kuantiti setiap data.
Misalnya, setiap sektor dalam carta pai di atas adalah sepadan dengan bilangan murid. Saiz sudut setiap sektor berkadaran dengan bilangan murid yang diwakili oleh setiap sektor.
Langkah-langkah di bawah menunjukkan cara-cara untuk membina carta pai.
Langkah 1
Hitung sudut bagi setiap sektor.
Langkah 2
Lukis sebuah bulatan dan bahagikan bulatan itu kepada sektor-sektor mengikut nilai-nilai sudut yang dihitung.
Langkah 3
Labelkan carta pai itu dengan tajuk yang sesuai dan labelkan petunjuk bagi setiap sektor.
Contoh
Warna
|
Merah
|
Biru
|
Hijau
|
Kuning
|
Bilangan pelajar
|
12
|
9
|
11
|
8
|
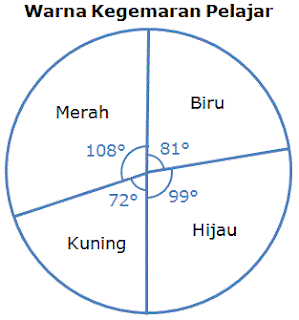
Jadual di atas menunjukkan warna kegemaran pelajar-pelajar dalam sebuah kelas. Wakilkan data-data tersebut dengan menggunakan carta pai.
Penyelesaian:
Memperoleh Dan Mentafsir Maklumat Daripada Carta Pai
Carta pai digunakan untuk mewakili data apabila perbandingan suatu kumpulan data dengan keseluruhan data lebih penting daripada nilai sebenarnya.
Daripada carta pai, kita boleh mentafsir maklumat dan seterusnya membuat kesimpulan.
Contoh
Hasil tinjauan tentang minuman panas yang digemari murid lelaki di SMKSI adalah seperti yang ditunjukkan dalam carta pai di atas.
a) Apakah minuman yang paling kurang digemari oleh murid lelaki SMKSI?
b) Apakah minuman yang paling digemari oleh murid lelaki SMKSI?
c) Berapakah peratus murid lelaki SMKSI yang menggemari minuman coklat?
Penyelesaian:
a) Kopi ialah minuman yang paling kurang digemari oleh murid lelaki SMKSI. [Sektor yang terkecil ialah kopi].
b) Teh ialah minuman yang paling digemari murid lelaki SMKSI. [Sektor yang terbesar ialah teh].
c) Peratus murid yang menggemari minuman coklat ialah: